What is Modulus Of Elasticity of Concrete? | Modulus Of Elasticity of Concrete Formula
What is Modulus Of Elasticity of Concrete? | Modulus Of Elasticity of Concrete Formula
Modulus Of Elasticity of Concrete
What is Modulus Of Elasticity of Concrete?
Concrete’s modulus of elasticity is determined by the moduli of elasticity of the aggregates and the cement matrix, as well as their relative quantities. It is defined as the ratio of normal stress to normal strain below a material’s proportional limit (modulus of elasticity Ec).
The modulus of elasticity of concrete remains largely constant at low stress levels but begins to decrease as matrix cracking develops at higher stress levels.
The elastic modulus of the hardened paste is typically between 10 and 30 GPa, while aggregates range between 45 and 85 GPa. The concrete composite then has a compressive strength of between 30 and 50 GPa.
Although concrete is not a fully linear-elastic material, Hooke’s law of elasticity holds true for the range of strains frequently utilized in design calculations.
The modulus of elasticity (Young’s Modulus) of concrete is a critical mechanical property. Elastic modulus is defined as the ratio of normal stress to corresponding strain for tensile or compressive stresses less than the material’s proportional limit.
It is a critical component affecting the structural performance of reinforced concrete structures and is especially useful as a design parameter for forecasting deformation in tall buildings.
Modulus Of Elasticity of Concrete Formula
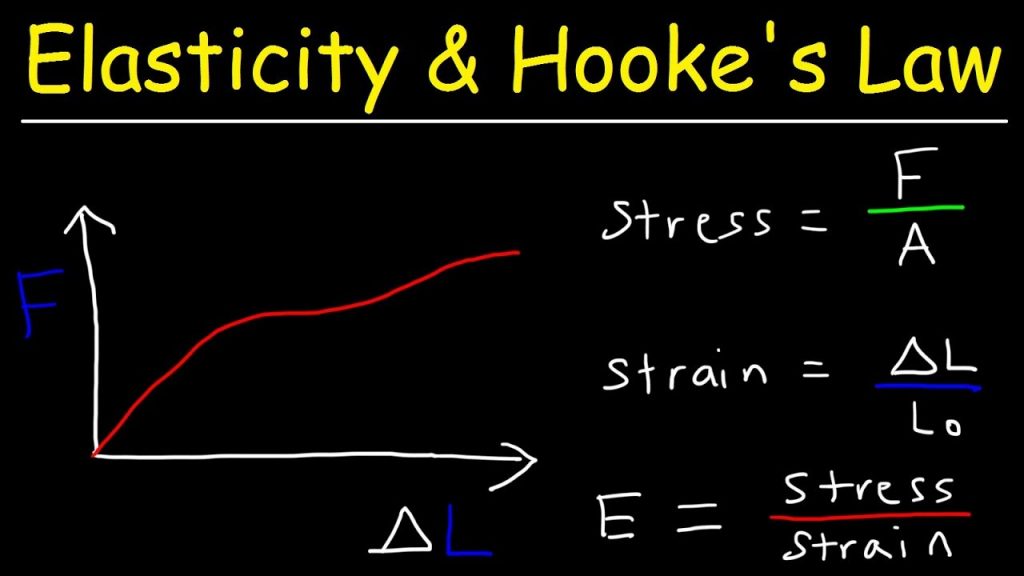
Hooke’s Law Formula
Typically, the modulus of elasticity of concrete is determined from the compressive strength of a concrete specimen. Stresses and strains are calculated and shown as a result of these strength tests.
On these graphs, the ratio of stress to strain is referred to as the modulus of elasticity, E. Due to the fact that concrete does not often behave linearly elastically, there is no region on the stress versus strain diagram where Hooke’s formula may be used to determine the modulus of elasticity.
s = Ee Hooke’s Law
(Where s denotes stress and e denotes strain).
Concrete’s modulus of elasticity is mostly determined by the coarse aggregate characteristics. Increase the modulus of elasticity of the concrete by increasing the size of coarse aggregates or by utilizing stiffer coarse aggregates with a higher modulus of elasticity.
Due to the fact that concrete is a composite material made of paste and aggregate, its modulus of elasticity in compression is highly dependent on the mechanical characteristics of the paste in comparison to the aggregate particles.
While stiffer or denser aggregates increase the elastic modulus of the concrete, they also have the potential to introduce stress concentrations at the transition zone and subsequent microcracking at the bond surfaces, hence reducing the concrete’s ultimate compressive strength capacity.
As the elastic moduli of the paste and aggregate particles approach unity, the resulting concrete exhibits a more linear stress-strain relationship and increases in brittleness. Two models are discussed that represent the two behavior boundaries of composite materials.
· The first model, an ideal composite hard material, is composed of filler particles with a low modulus of elasticity that are connected by an elastic phase matrix with a high modulus of elasticity.
· The second model, an ideal composite soft material, is composed of filler particles with a high modulus of elasticity and an elastic phase matrix with a low modulus of elasticity.
High-strength concretes would more nearly resemble the first of the two idealized models, and conventional-strength concretes would more closely resemble the second.
The relationship between compressive strength and other mechanical parameters of high-strength concretes exhibits a substantial variance in behavior with regard to early strength.
Compressive strength often increases faster than bond strength in the interfacial transition zone. This results in proportional changes in elastic modulus and tensile strength between early and late ages.
As a result, the relationship between mechanical characteristics and later age compressive strength (28 days or later) of high-strength concrete cannot be expected to hold true as it does for conventional-strength concrete.
In general, the modulus of elasticity of conventionally reinforced concrete grows according to the square root of the compressive strength.
While numerous empirical equations for estimating modulus of elasticity have been proposed, few of these equations accurately predict the modulus of elasticity of high-strength concrete.
Importance of Modulus of Elasticity of Concrete
Elastic modulus is a critical mechanical property of concrete. The modulus value indicates the stiffness of the material.
Thus, when a high-performance concrete is compared to a regular strength concrete, the elastic modulus of the high-performance concrete is greater, indicating that it is a stiffer type of concrete.
Stiffness is a desired quality for concrete since it reduces the amount of deflection that a structure may undergo. However, in high strength concrete, deformations such as creep increase.